A Wikipédia látogatói egyszer észrevették, hogy ha rákattint az egyes cikkek első linkjére, előbb vagy utóbb még mindig a filozófia szentelt cikkek egyikébe ugrik. Ennek a jelenségnek a magyarázata nagyon egyszerű: a modern kultúra, a tudomány és a technológia szinte minden eredményét filozófiai elméletek és paradoxonok alapján teremtik meg, immár immáron.
Ebben a cikkben gyűjtöttünk össze néhány olyan kíváncsi példát és történetet, amelyet a filozófusok illusztráltak ötleteikre. Sokan több mint kétezer évesek, de még mindig nem veszítik el jelentőségüket.
Buridanov szamár
Buridanov szamara egy filozófiai paradoxon, amelyet Jean Buridan neveztek el, annak ellenére, hogy Arisztotelész műveiből ismert.
A szamár két, teljesen azonos mészkocsit talál. Nem tud választani közülük, elveszíti az időt, értékeli az egyes lehetőségeket. A késés miatt a szamár éhezik, és a megoldás ára egyre nő. És ha nem tud választani az egyenértékű lehetőségek közül, a szamár végül meghal az éhség miatt.
Ez a példa természetesen az abszurditás pontjára vezethető vissza, de tökéletesen illusztrálja, hogy néha a választás szabadsága a szabadság teljes hiányát eredményezi. Ha megpróbálod mérlegelni a leginkább racionálisan hasonló lehetőségeket, mindkettőt elveszítheted. Ebben az esetben minden lépés jobb, mint az optimális megoldás végtelen keresése.
A barlang mítosza
A barlang mítosza a híres allegória, amelyet Platón használ az “Állami” párbeszédben, hogy megmagyarázza az elképzeléseinek tanát. A platonizmus és az objektív idealizmus sarokkövének számít.
Képzeljünk el egy törzset, amelyet elítéltek egy mély barlangban élni. A tagok lábán és kezén olyan láncok vannak, amelyek megakadályozzák a mozgását. Ebben a barlangban több nemzedék született, az egyetlen tudásforrás, amelyhez a fény elhalványodik, és a felszínről érző érzéketlen hangok hallatszanak.
Most képzeld el, hogy ezek az emberek ismerik az életet kívülről?
És egyikük levette a bilincsét, és eljutott a barlang bejáratáig. Látta a napot, a fákat, a csodálatos állatokat, a madarakat az égen. Aztán visszatért társainak, és elmondta nekik, mit látott. Hinnék neki? Vagy inkább hitelesek lesznek azok a sötét kép az alvilágról, amelyet saját szemükkel látnak minden életükben?
Soha ne dobd el az ötleteket, mert úgy tűnt, abszurd neked, és nem illeszkednek a világ ismerős képébe. Talán minden tapasztalata csak egy homályos visszaverődés a barlang falán.
A mindenhatóság paradoxonja
Ez a paradoxon abban áll, hogy megpróbálja megérteni, hogy egy teremtmény képes-e bármilyen cselekvést végrehajtani, olyan dolgot, amely korlátozza cselekvési képességét.
Egy mindenható teremtmény olyan kővé válhat, amelyet önmagában nem tud felemelni?
Talán azt fogja találni, hogy ez a filozófiai feladat tisztán spekulatív kényeztetés, teljesen elvált az életből és a gyakorlatból. Ez azonban nem így van. Az omnipotencia paradoxonának nagy jelentősége van a vallás, a politika és a közélet számára.
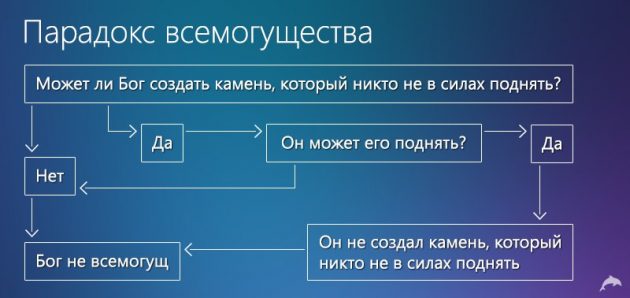
Míg ez a paradoxon megoldatlan marad. Csak feltételezhetjük, hogy nincs abszolút mindenhatóság. Így mindig van esélyünk a győzelemre.
A csirke és tojás paradoxonja
Valószínűleg mindenki hallott erről a paradoxonról. Ez a probléma első ízben az ókori Görögország klasszikus filozófusainak munkásságában jelent meg.
Mi volt azelőtt: csirke vagy tojás?
Első pillantásra a feladat úgy tűnik, hogy oldhatatlan, mivel egy elem megjelenése lehetetlen egy másik létezése nélkül. Azonban a paradoxon összetettsége homályos megfogalmazásban rejlik. A probléma megoldása attól függ, hogy mi szerepel a “csirke tojás” fogalmával. Ha egy csirke tojás egy tojás, amelyet egy csirke összetört, akkor az első természetesen nem egy csirke tojásból keltetett csirke volt. Ha egy csirke tojás olyan tojás, amelyből egy csirke nyílik, akkor az első csirke tojás volt, amelyet nem csirke füstölt.
Minden alkalommal, amikor szembe kell néznie egy megoldhatatlan feladattal, figyelmesen olvassa el a feltételeket. Néha ez a hely, ahol a válasz útja fekszik.
Achilles és a teknős
Ez a paradoxon az Elea Zenon – egy ősi görög filozófus, az Eleatic iskola híres képviselője. Segítségével megpróbálta bizonyítani a mozgás, a tér és a készlet ellentmondásosságát.
Tegyük fel, hogy Achilles 10-szer gyorsabban fut, mint egy teknős, és mögötte 1000 lépésnyire van. Míg Achilles végigjárja ezt a távolságot, a teknős 100 lépésnyire mozog ugyanabba az irányba. Amikor Achilles 100 lépésből áll, a teknős több 10 lépésből áll, és így tovább. A folyamat határozatlan ideig folytatódik, Achilles soha nem fog felzárkózni a teknősbe.
Ennek a kijelentésnek a puszta abszurditása ellenére sem könnyű ellene megcáfolni. Megoldást találni végzett komoly vita épített különféle fizikai és matematikai modellek, cikkeket írnak és disszertációk védett.
Számunkra a probléma levonása nagyon egyszerű. Még akkor is, ha minden tudományos lámpatest ragaszkodik ahhoz, hogy soha ne találkozzon teknősvel, ne add fel. Csak próbáld meg.